Se sta piovendo, ci si bagnerà di più correndo o camminando verso un rifugio? Si può dimostrare che la risposta dipende dalla direzione di caduta della pioggia (verticale o diagonale) e dalla direzione verso cui ci si sta muovendo.
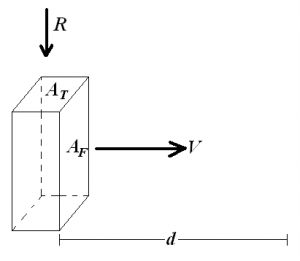
Immaginiamo di trovarci (malauguratamente) sotto ad un diluvio con in mano una spugna: questa sarà il nostro metro di riferimento per valutare se ci siamo bagnati tanto o poco. Prendiamo quindi una spugna rettangolare che si muove a velocità 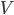 verso destra. Supponiamo che le gocce di pioggia cadano verticalmente ad una velocità
verso destra. Supponiamo che le gocce di pioggia cadano verticalmente ad una velocità 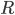 . Le due aree della spugna saranno rispettivamente
. Le due aree della spugna saranno rispettivamente 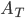 e
e 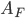 .
. 
Assumiamo che il numero totale delle gocce di pioggia per volume (concentrazione) sia 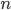 e costante. Il flusso di gocce di pioggia che incidono sulla spugna dall'alto (ovvero il numero di gocce di pioggia che cadono sulla parte superficiale della spugna per secondo) è dato da
e costante. Il flusso di gocce di pioggia che incidono sulla spugna dall'alto (ovvero il numero di gocce di pioggia che cadono sulla parte superficiale della spugna per secondo) è dato da
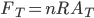
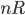 tiene conto del numero di gocce che cadono alla velocità
tiene conto del numero di gocce che cadono alla velocità 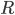 in un certo volume, moltiplicando per l'area della spugna
in un certo volume, moltiplicando per l'area della spugna 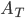 si ottengono proprio le gocce che cadono sopra alla spugna. Notate che questo valore è indipendente dalla velocità della spugna, e quindi dalla vostra velocità. Similmente il flusso delle gocce di pioggia sull'area
si ottengono proprio le gocce che cadono sopra alla spugna. Notate che questo valore è indipendente dalla velocità della spugna, e quindi dalla vostra velocità. Similmente il flusso delle gocce di pioggia sull'area 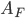 è
è 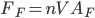
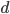 , allora il tempo per arrivarci è
, allora il tempo per arrivarci è 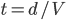 (dato che ci muoviamo a velocità
(dato che ci muoviamo a velocità 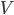 ). Il numero totale di gocce che entrano nella spugna durante questo tempo è
). Il numero totale di gocce che entrano nella spugna durante questo tempo è 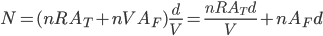
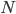 è la somma delle gocce che cadono sulla parte superiore della spugna e sulla parte frontale, durante il tempo
è la somma delle gocce che cadono sulla parte superiore della spugna e sulla parte frontale, durante il tempo 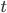 . Quindi
. Quindi
il numero totale di gocce che entrano dalla parte frontale NON dipende dalla velocità della spugna; il numero totale di gocce che entrano invece dalla parte superiore dipende inversamente dalla velocità: più la spugna si muove lentamente, più gocce entreranno nella spugna dall'alto.
Quindi, muovendosi più velocemente, si minimizza il numero di gocce che ci bagnano: anche se l'aumento di velocità causa una maggiore raccolta di gocce frontalmente, il tempo impiegato per arrivare al rifugio è minore quindi ci si bagna nello stesso modo sul davanti, mentre superiormente il numero di gocce raccolte è minore! Quindi la velocità è importante solo per stabilire il numero di gocce che ci cascano in testa: più ci muoviamo lentamente e più ne raccoglieremo. Infatti il ragionamento fatto per una spugna rettangolare si può fare per un corpo di forma qualsiasi, a patto di identificare due aree 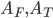 .
.
E se la pioggia cadesse in diagonale?
Se la pioggia cade ad un angolo dovuto ad una certa velocità del vento 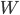 , dobbiamo utilizzare la velocità relativa
, dobbiamo utilizzare la velocità relativa 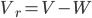 per calcolare il flusso di gocce che incidono sulla spugna
per calcolare il flusso di gocce che incidono sulla spugna
che è dato da
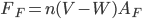
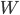 opposta a
opposta a 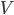 , ovvero con
, ovvero con 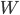 negativa). Se
negativa). Se 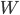 è positiva, e più grande di
è positiva, e più grande di 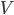 (ovvero il vento si muove più velocemente di noi), allora il flusso di gocce frontalmente è negativo. Fisicamente, questo significa che le gocce colpiranno con più probabilità il retro della spugna, piuttosto che la parte frontale, e questo renderebbe la spugna ugualmente bagnata. Per tenere conto di tutti i casi, dobbiamo ignorare i segni e prendere quindi il valore assoluto della differenza tra le due velocità
(ovvero il vento si muove più velocemente di noi), allora il flusso di gocce frontalmente è negativo. Fisicamente, questo significa che le gocce colpiranno con più probabilità il retro della spugna, piuttosto che la parte frontale, e questo renderebbe la spugna ugualmente bagnata. Per tenere conto di tutti i casi, dobbiamo ignorare i segni e prendere quindi il valore assoluto della differenza tra le due velocità 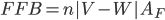
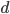 stavolta è
stavolta è 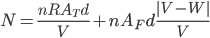
 allora questo termine sparisce, e l'unico flusso sarebbe quello nella parte superiore della spugna!
allora questo termine sparisce, e l'unico flusso sarebbe quello nella parte superiore della spugna!
Quindi, mentre state cercando rifugio durante un temporale, che la pioggia cada verticalmente o obliquamente verso di voi, per stare asciutti il più possibile dovrete muovervi il più veloce possibile verso il primo luogo riparato. In presenza di un vento in coda, l'unico modo per bagnarsi il meno possibile sarà quello di muoversi verso il rifugio alla stessa velocità del vento.
..da un'idea della prof.ssa De Caria (Millersville University)

L'ho sempre pensato e ho sempre avuto la percezione che affrettandomi sotto la pioggia mi sarei bagnato di meno, anche se non ne avevo la certezza. Ora non ho dubbi. Speriamo però che domani non piova che vado a cogliere le olive.
bel lavoro